Magnetic Domain Inflection – Charge Admittance

Concept Summary

A sprit (σ) — the fundamental charge acceleration event — perturbs not just local electric fields but also the surrounding magnetic domain structure. Unlike classical magnetic field models that assume a fixed background permeability ( $\mu_0$ ), the Charge Admittance (CA) framework treats magnetic domains as dynamic responses to energy structuring events.

The response of the medium is encoded in variations in the admittance tensor $\Xi(\vec{r}, t)$ , which shapes the electromagnetic field response in both direction and coherence.

Key Expression:

$\delta \Xi(\vec{r}, t) = f\left( \nabla \cdot \vec{B}_\Xi, \ \nabla \times \vec{E}_\Xi \right)$

This states that variations in local field admittance are a function of:

The divergence of the magnetic field (normally zero in Maxwell’s equations, but locally perturbed here)
The curl of the electric field, which reflects induced magnetic activity during energy propagation

Interpretation:

The change in the medium’s structural impedance, $\delta \Xi$ , reflects a field lensing effect — similar to how optical lenses bend light.
Regions of strong $\nabla \cdot \vec{B}_\Xi$ indicate disrupted magnetic symmetry, typical near sprit (σ) events.
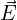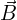The dynamic interplay between $\vec{E}$ and $\vec{B}$ causes magnetic domain “fuzzing,” realigning their topology.

Implication:

Instead of assuming magnetism as a background state, CA treats magnetic domains as secondary responses to charge-induced energy structuring. Magnetic inflection points act as impedance contours in the field — bending, distorting, or refocusing energy flow similar to wavefront behavior in optics.

This view provides a physical basis for:

Magnetic memory
Domain wall motion
Hysteresis as structural lag in $\Xi$