A Thought Experiment Involving Ballistics
From the summit of an impossibly high mountain, Newton imagined a cannon firing a projectile horizontally.
Subluminal Velocity (A and B): At lower velocities, the cannonball follows a parabolic path, eventually succumbing to the inexorable pull of gravity and crashing to earth.
Orbital Velocity (C and D): At a critical velocity, the curvature of the projectile’s path matches the curvature of the Earth. The cannonball continues to fall, but it never reaches the ground, instead circling the Earth in a perpetual orbit.
Escape Velocity (E): As the cannonball’s velocity is increased, the parabola elongates, and the projectile travels greater distances before landing.
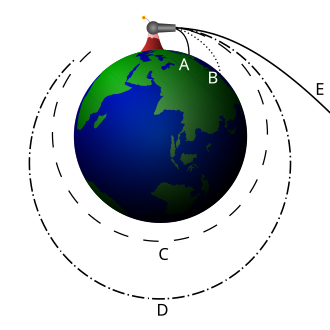
Newton’s thought experiment elegantly illustrates the fundamental unity of terrestrial and celestial mechanics. It demonstrates that the same force that causes an apple to fall from a tree also governs the motion of the Moon around the Earth.
Within the context of the Z0-Field, Newton’s cannonball offers a compelling analogy:
Gravity, in the Z0 Field, is analogous to the gradients in μ0ε0 that guide the flow of energy.
Orbiting cannonballs are analogous to stable energy configurations within the Z0 Field, perhaps representing particles or larger structures.
This perspective suggests that what we perceive as gravity is not a separate force, but rather a manifestation of the μ0ε0 Field’s geometry and energy dynamics.
