Concept Summary
When a sprit (σ – a localized charge acceleration-deceleration event) occurs, it emits energy into the field as electromagnetic radiation. In classical electrodynamics, this emission is described by the Poynting vector:
![\[ \vec{S}_\Xi = \frac{1}{\mu_0(\vec{r}, t)} \vec{E}_\Xi \times \vec{B}_\Xi \]](https://gravityz0.com/wp-content/ql-cache/quicklatex.com-e2a64ec09465b117c2a8ef8707fe0528_l3.png "Rendered by QuickLaTeX.com")
However, under Charge Admittance (CA), the vacuum is no longer a passive medium. The local structure of the vacuum is encoded in the admittance tensor 
, which modifies the character of both the electric and magnetic field components.
Modified Poynting Vector Equation:
Where the modified field vectors are:
![\[ \vec{E}_\Xi = \Xi(\vec{r}, t) \cdot \vec{E}_{\text{classical}} \]](https://gravityz0.com/wp-content/ql-cache/quicklatex.com-ae8d2cee077a3e4a20cb14f8465bd514_l3.png "Rendered by QuickLaTeX.com")
![\[ \vec{B}_\Xi = \Xi(\vec{r}, t) \cdot \vec{B}_{\text{classical}} \]](https://gravityz0.com/wp-content/ql-cache/quicklatex.com-bcf01959fab22e29de3cb0ae272ae85d_l3.png "Rendered by QuickLaTeX.com")
Interpretation:
- The tensor
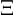acts like a directional filter or local “coherence weighting” that reshapes how energy exits the sprit (σ). - In strongly coherent regions,
(the identity tensor), and classical behavior is recovered. - In highly anisotropic regions (e.g., around other structured events), energy radiation may become distorted or directionally preferred.
- This generalizes the Poynting flow beyond vacuum solutions, introducing a path for explaining phenomena like field shadowing, coherence collapse, or apparent energy anisotropies.
Implication:
This reinterpretation enables a richer understanding of field emission near complex energy events — moving beyond the simple vector cross-product to an impedance-modulated, structure-aware formulation.