Field Memory and Coherence Persistence

Concept Summary

In the Charge Admittance (CA) framework, the vacuum is not an empty, passive stage — it is a structured, responsive medium that remembers the influence of past energy events. Every sprit (σ – localized charge acceleration-deceleration) impresses a signature onto the lattice. That signature fades over time, but its persistence defines coherence — the ability of a region to sustain phase-locked responses to new stimuli.

This leads to a measurable field memory, which governs phenomena like interference patterns, standing waves, and quantum entanglement.

Key Expression:

    \[ \mathcal{C}(\vec{r}, t) = \int_{t_0}^{t} \left| \nabla \Xi(\vec{r}, t') \right|^2 e^{-\lambda(t - t')} dt' \]

Where:

  • \mathcal{C}(\vec{r}, t) is the coherence memory function
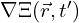  • \nabla \Xi(\vec{r}, t') describes local structural gradients in the field admittance tensor
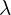  • \lambda is a decay constant, capturing how quickly coherence fades
  • The integral spans from the initial event time 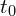t_0 to the current time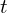 t

Interpretation:

This model supports the idea that space is not instantaneous. Instead, its structure is layered by historical field activity:

  • Quantum coherence is reinterpreted as sustained alignment in the field lattice.
  • Entanglement can be understood as shared structure in high-\mathcal{C} regions, not instant communication.
  • Measurement effects occur when new field inputs decohere a previously stable structure.

Field memory is the scaffold on which energy-time structure — and causality — are built.