Time : A Consequence of Energy Flow
Abstract
In the Charge Admittance (CA) framework, While time appears a universal, linear background it is a fleeting conditional consequence of energy propagation through a non-uniform field lattice defined by local ε₀ and μ₀ variation. This section introduces the Conservation of Time, a proposed principle asserting that time emerges only in the presence of energy gradients and ceases when those gradients resolve. Time becomes a function of the energy barycenter’s displacement over an admittance-defined path. This reframing allows for a quantifiable, testable connection between local field dynamics and time itself.
Time as an Emergent Gradient Metric
Rather than treating time as a fundamental dimension or an independent parameter, we define time (t) as a field-dependent artifact:
(1) 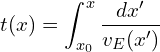
Where:
- vE(x′): local energy propagation speed, a function of the local permittivity and permeability:
(2) 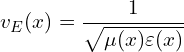
- x0: origin of energy emission or perturbation.
- x: current location of the energy barycenter.
Thus, time is not absolute — it is defined by the path-integrated inverse energy velocity through the field. No energy propagation → no passage of time.
Conservation of Time Principle
Postulate:
Time exists only when energy is actively propagating through a non-uniform field. In the absence of a spatial gradient in field admittance, energy does not move — and time does not progress.
From this we assert the Conservation of Time:
(3) ![]()
Where 𝒯 is defined as the “temporal state” of a region — a scalar metric proportional to cumulative energy displacement within that field over time. In flat admittance regions (no ε₀, μ₀ gradients), the system experiences no net time evolution.
Causal Relationship Between Energy and Time
We define a Time-Energy Causality Function (TEC) as:
(4) ![]()
This relation frames causality itself as dependent on local field conditions, not external clock time. A fixed spatial distance r takes different “amounts of time” to traverse depending on the local impedance.
This echoes gravitational time dilation but grounds it in measurable admittance variation, not spacetime geometry.
Testable Predictions and Experiments
Time Delay in Engineered Admittance Fields
Experiment: Create a variable-permittivity dielectric chamber and propagate coherent light pulses through it.
- Prediction: Measurable differences in time-of-flight as field impedance varies.
- Setup: Compare clock time inside and outside the chamber using atomic clocks or interferometry.
Temporal Collapse in Field Relaxation
Experiment: Monitor systems undergoing gradient decay (e.g., cooling plasma).
- Prediction: A corresponding plateau in time evolution of correlated wave behaviors as energy flow flattens.
Quantized Time Domains
Hypothesis: In regions of discrete field lattice spacing, time will exhibit quantized behavior linked to nodal energy resonance.
- Prediction: Detectable oscillatory intervals in photon emission timing or particle decay.
Implications for Cosmology and Quantum Theory
- Beginning of Time: In CA, “time begins” wherever energy condenses into a field structure. No energy → no time.
- End of Time: If the universe tends toward field homogeneity, time may asymptotically halt — a “thermal time death” reframed as admittance flattening.
- Entanglement: Two particles may remain in temporal sync not through spooky action, but shared coherent admittance gradients.
Summary
This echoes gravitational time dilation but grounds it in measurable admittance variation, not spacetime geometry.
This model:
- Bridges gravity, redshift, and time dilation with field theory.
- Replaces curvature with impedance.
- Predicts measurable field-based timing effects that could reshape our understanding of clocks, causality, and cosmogenesis.
