Energy-Based Field Equation

This is a proposed modification of the Einstein Field Equation, substituting energy propagation effects for mass-driven curvature. The coupling constant now depends on the electromagnetic properties of the vacuum:

$R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R + \Lambda g_{\mu\nu} = \frac{8\pi}{c^4 \mu_0 \varepsilon_0} \, \mathcal{E}_{\mu\nu}$

Where:

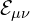$\mathcal{E}_{\mu\nu}$ represents the energy-flow tensor, replacing the traditional mass-energy tensor.
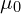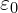$\mu_0$ , $\varepsilon_0$ are spatially variable vacuum parameters controlling energy propagation speed.
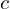$c$ is locally defined as 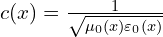$c(x) = \frac{1}{\sqrt{\mu_0(x)\varepsilon_0(x)}}$ , not a constant.

This version proposes that spacetime curvature results from gradients in energy density and propagation speed rather than from the presence of mass. The energy-based tensor $\mathcal{E}_{\mu\nu}$ may generalize electromagnetic stress and flux propagation within variable field impedance.